MRIの撮像において、k-spaceにおけるフィルタ処理(いわゆるRawDataフィルタ)と空間領域におけるフィルタ処理(いわゆるImageフィルタ)があります。その効果を、臨床像の視覚評価で行なおうとしても、被写体の個体差や観察者の主観の影響から、一定した結果は得られないように思われます。
フィルタの特性の客観的評価の試みとして、MRI画像の2次元空間周波数スペクトル分布とウィナースペクトルを測定してみました。
|
方 法 |
|
| 1 |
【 使用機器 】 1.MRI装置 : Avant(1.5T,SIEMENS) |
| 2 |
【 主なシーケンス・パラメータ 】 T1WIのスピンエコー法を用いました。主なパラメータは以下のとおりです。 |
| 3 |
【 2次元空間周波数スペクトル 】 1.装置付属の球ファントムの横断像を撮影 |
| 4 |
【 ウイナースペクトル 】 1.装置付属の球ファントムの横断像を撮影 2.画像中央の均一な領域にROIを設定 2.ROI内を多数のセグメントに分割 3.セグメントのそれぞれについてフーリエ変換、パワースペクトルを求める 4.パワースペクトルを面積で規格化、ウィナースペクトルとする 5.全ウィナースペクトルの加算平均し、求めるウィナースペクトルとした *一連の計算を、自作ソフトにて行いました。統一した条件で容易に計算可能です。(そのソフトについて) |
| 5 |
|
|
K-Spaceにおけるフィルタ特性 |
|||
|
|
|||
| 1 |
フィルタを使用しない時の2次元空間周波数絶対値スペクトル : スペクトル分布の外周まで、連続した広がりとなりました。 AcquisitionMatrix;256,NumberOfPhaseEncodingSteps;256,PercentPhaseFieldOfView;100 |
||
| 2 |
|
||
| 3 |
Ellipseフィルタを使用した時の2次元空間周波数絶対値スペクトル : Ellipseフィルタを使用すると、原点を中心とし、等方性に外周の輝度が低下しました。 ほぼ円形のスペクトル分布となりました。 AcquisitionMatrix;256,NumberOfPhaseEncodingSteps;256,PercentPhaseFieldOfView;100  |
||
| 4 |
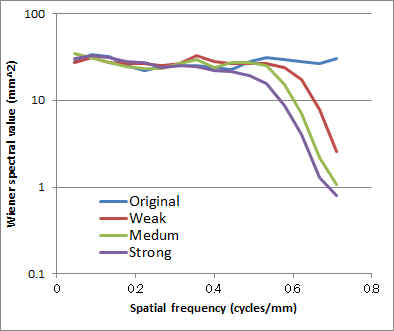
|
RawDataフィルタの設定を変えたときのウィナースペクトル
: Originalのウィナースペクトルカーブ形状には周波数依存性が無く、ホワイトノイズとみなせます。 |
|
| 5 |
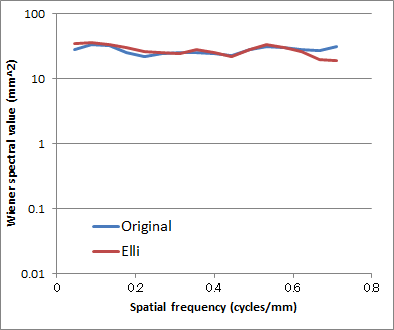
|
Ellipseフィルタの設定を変えた場合のウィナースペクトル: Originalとほぼ一致しました。 |
|
| 6 |
Ellipseフィルタ使用では、左右方向の端部(高周波端)で減衰がみられましたが、上下方向はOriginalとほぼ等しくなりました。 3者とも、Window条件を固定して表示してあります。 |
||
| 7 |
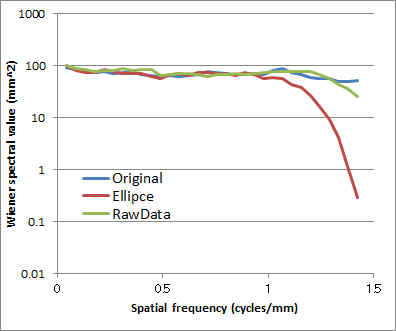 |
”収集マトリックス>位相エンコード数”における周波数エンコード方向のウィナースペクトル: |
|
| 8 |
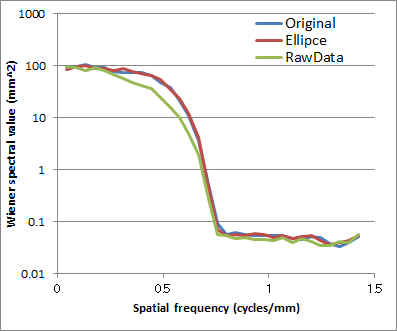 |
”収集マトリックス>位相エンコード数”における位相エンコード方向のウィナースペクトル |
|
|
|
|||
|
空間領域におけるフィルタ特性 |
|||
|
|
|||
| 1 |
Imageフィルタを使用した時の2次元空間周波数絶対値スペクトル : lImageフィルタを使用すると、ほぼ全周波数領域の輝度が変化しました。 |
||
| 2 |
|
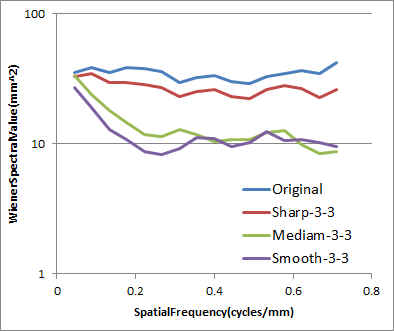
ImageフィルタのIntensityを変化させたときのウィナースペクトル
:
Sharp、Mediam、Smoothの順で低下しました。SharpとMediam間の差が大きく、MediamとSmooth間の差は小さなものでした。 |
|
| 3 |
|
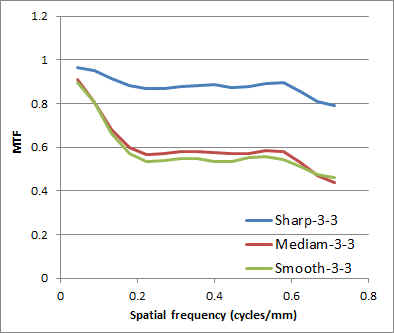
Original画像のノイズをホワイトノイズとみなしました。Avantは、オリジナル画像とフィルタ画像が同時に取得できるので、それぞれの絶対値スペクトルを求め、その比をMTFとしました。
全周波数域でIntensityの違いに応じ、低下しまた。MediamとSmoothは、ほぼ等しくなりました。 |
|
|
Imageフィルタは、空間周波数の広い範囲で効果があり、ノイズ低減に有効ですが、同時に信号成分も減衰することになり、撮影部位、個体差、観察者により評価が分かれることになるでしょう。 |
|||
以上